5. Kombinační logické obvody

• Analýza kombinačního obvodu, jeho přepis do pravdivostní tabulky a logické funkce
• Návrh kombinačního obvodu z pravdivostní tabulky a z logické funkce

---

Kombinační obvod

• U těchto obvodů je výstup určen výhradně kombinací vstupních veličin. Hodnoty výstupních veličin nezávisí na předcházejícím stavu logického obvodu, což znamená, že kombinační logický obvod neobsahuje žádné paměťové prvky.
• Nemá paměť - jeho výstupní proměnné jsou jednoznačně určeny pomocí vstupních hodnot.
• Kombinační obvody jsou klíčové pro realizaci řady digitálních funkcí. Jejich návrh vyžaduje znalost Booleovy algebry a schopnost optimalizovat logické výrazy. V praxi se kombinační obvody často implementují ve formě integrovaných obvodů, jako jsou multiplexery nebo aritmeticko-logické jednotky (ALU).

Analýza kombinačního obvodu, jeho přepis do pravdivostní tabulky a logické funkce

• Předurčení analýzy kombinačního obvodu

  • Předurčení analýzy kombinačního obvodu znamená přípravu a určení metod, které budou použity k rozboru daného obvodu. Cílem je zjistit, jak obvod funguje na základě jeho vstupních a výstupních proměnných.
    
    
  • Před samotnou analýzou je nutné:
    • Identifikovat typ obvodu – zda jde například o dekodér, multiplexor, aritmetický obvod (např. sčítač) apod.
    • Zjistit počet vstupů a výstupů – to ovlivní složitost analýzy.
    • Vybrat metodu analýzy – například použití pravdivostní tabulky, Karnaughovy mapy nebo Booleovy algebry.
    • Ověřit logické funkce – například kontrolou zapojení jednotlivých logických hradel.

• Postup analýzy kombinačního obvodu na příkladu

  1. Identifikace součástí
     • Rozpoznání logických hradel (AND, OR, NOT, NAND, NOR, XOR)
     • Určení vstupů a výstupů obvodu
     • Identifikace propojení mezi hradly
  2. Systematická analýza
     • Postupovat od vstupů k výstupům
     • Označit mezivýsledky na větvích obvodu
     • Analyzovat každé hradlo samostatně
  3. Matematický popis

     • Zapsat logické funkce pro jednotlivá hradla

     • Postupně skládat dílčí funkce

     • Vytvořit celkovou funkci obvodu

  • XOR

    
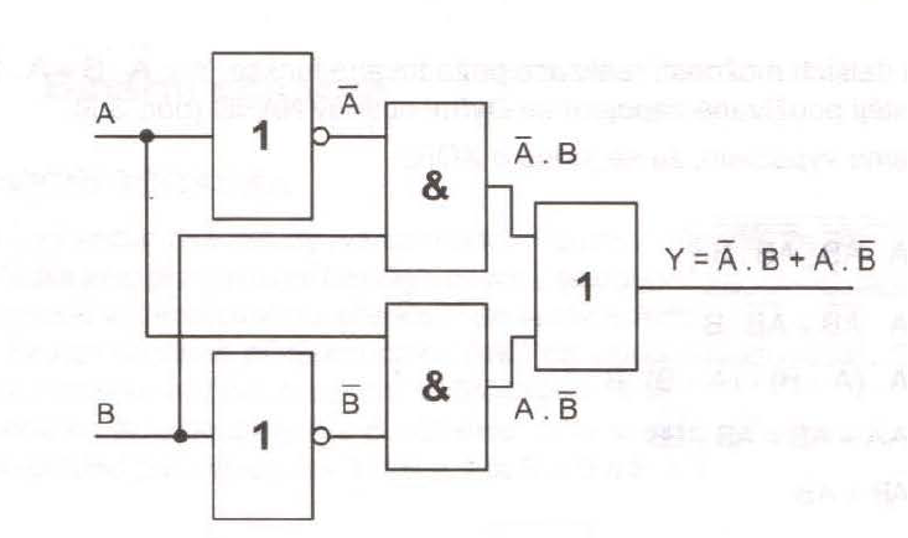
    1. Identifikace součástí:
       • Obvod má 2 vstupy: A a B.
       • Obvod má 1 výstup: Y.
       • Používáme XOR hradlo, což znamená, že výstup Y bude: $Y=A\oplus B$, kde $\oplus$ označuje operaci XOR.
    2. Určení logického výrazu:
       • XOR hradlo produkuje výstup 1 pouze tehdy, když je pouze jeden z vstupů 1, ale ne oba.
       • Logický výraz pro tento obvod bude: $Y=A\oplus B=(A\cdot \overline{B})+(\overline{A}\cdot B)$.
       • To znamená, že výstup bude 1, pokud A a B mají různé hodnoty. 
    3. Tvorba pravdivostní tabulky:
       • Postup vytvoření pravdivostní tabulky:
         1. Určit počet vstupů a vytvořit všechny kombinace
         2. Postupně vyhodnotit jednotlivá hradla
         3. Zapsat mezivýsledky do tabulky
         4. Určit konečný výstup pro každou kombinaci
       • Vytvoříme pravdivostní tabulku pro všechny možné kombinace vstupních hodnot A a B. Pro XOR hradlo to bude vypadat takto:
         
         
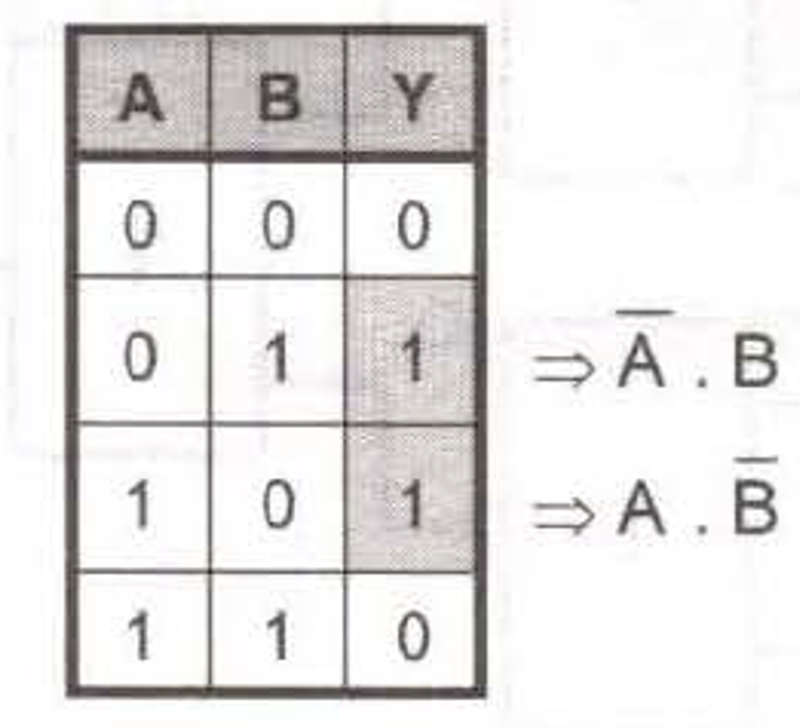
       • Vysvětlení pravdivostní tabulky:
         • Když jsou oba vstupy stejné (0,0 nebo 1,1), výstup je 0.
         • Když jsou oba vstupy různé (0,1 nebo 1,0), výstup je 1.
           
           
    4. Zjednodušení logického výrazu:
       • V tomto případě již máme jednoduchý logický výraz pro XOR obvod, který je: $Y=(A\cdot \overline{B})+(\overline{A}\cdot B)$
       • Tento výraz je již v optimální podobě, protože nelze dále zjednodušit.

---

Návrh kombinačního obvodu z pravdivostní tabulky a z logické funkce

• Mezi základní kombinační obvody patří:

  • XOR
  • Poloviční sčítačka
  • Kodéry a dekodéry
  • Multiplexery a demultiplexery

• Chování logického obvodu je zpravidla určeno tabulkou, která obsahuje stavy vstupních a výstupních proměnných.

• Nejdůležitější je určit počet vstupních a výstupních proměnných daného obvodu, označit je a přiřadit jim logické hodnoty 0/1.
  
  

• Postup zjednodušování výrazu:

  • Z pravdivostní tabulky sestavíme logickou funkci podle algebraického výrazu (konjunktivním nebo disjunktivním tvar).
  • Tabulkově sestavená funkce bývá často správná, ale zároveň zbytečně složitá. Pro zajištění co nejjednodušší, spolehlivé a cenově efektivní konstrukce logického obvodu je nutné provést její minimalizaci, k čemuž existuje několik metod.
  • Jako nejčastější zjednodušení daného výrazu se používá zjednodušení pomocí Booleovy algebry, nebo také pomocí Karnaughovy mapy.
    
    
  • Musíme také myslet na logické prvky, ze kterých chceme obvod sestavit. Obvody mohou být sestaveny jako:
    • Kontaktní - tlačítek, relé, spínačů, stykačů…
    • Bezkontaktní - dnes jsou realizovány pomocí číslicových integrovaných obvodů, jednočipových mikropočítačů nebo PLC.

  • XOR

    • Nejpoužívanější kombinační obvod - někteří ho řadí mezi základní logické obvody.
    • Exclusive OR, EX-OR, X
    • OR, nerovnost, nonekvivalence, sčítačka modulo 2 atd..
      
      

    • Postup sestrojení

      1. Vytvoříme obvod, aby splňoval sčítání ve dvojkové soustavě:
         
         $$\begin{array}{rl}0+0& =0\\ 0+1& =1\\ 1+0& =1\\ 1+1& =0\end{array}$$
      2. Sestrojíme pravdivostní tabulku:
         • Z druhého a třetího řádku této tabulky vyplývá základní součtový tvar funkce: Y = A x B + A x B.
           
           
      3. Sestrojíme blokové schéma:
         
         

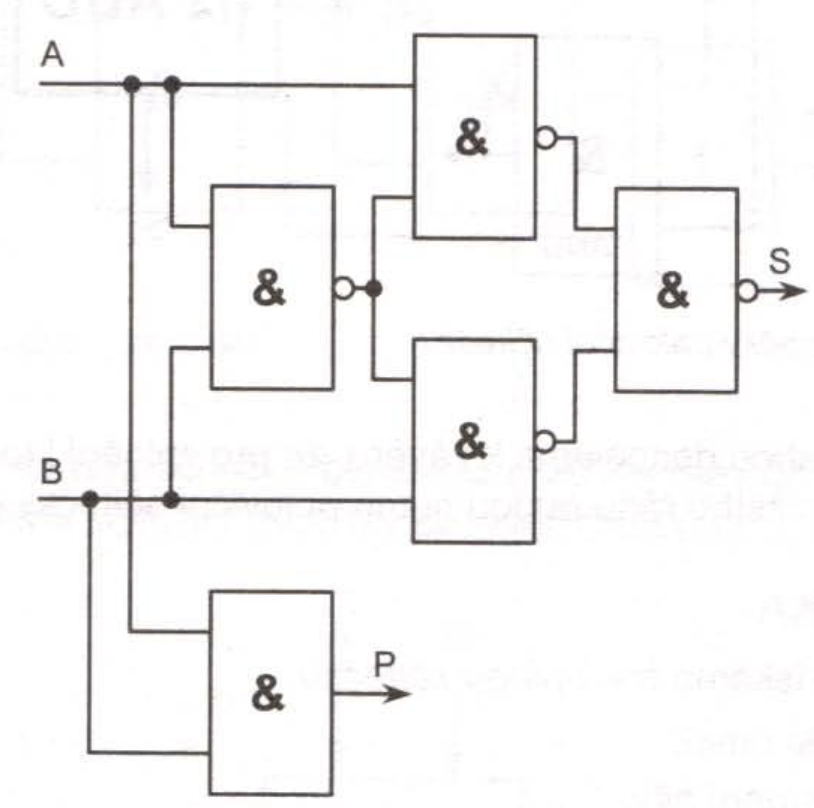
• Poloviční sčítačka

  • Poloviční sčítačka XOR umí sečíst dva vstupy (vstupní bity). Pouze v případě, Že oba vstupy jsou rovny 1 (čtvrtý řádek jeho pravdivostní tabulky), dovede sice vypočítat součet 1 + 1 = 0, ale nedovede vygenerovat tzv. přenos P do vyššího řádu. Této funkce docílíme přidáním členu AND na vstup obvodu XOR. Získáme tak zapojení, které se nazývá poloviční sčítačka.
  • Přenost do vyššího řádu = carry.