1. Minimalizace logické funkce algebraická a grafická

Předurčení minimalizace logické funkce
Algebraická minimalizace logické funkce na příkladě
Grafická minimalizace logické funkce na příkladě

Předurčení minimalizace logické funkce

Minimalizace logických funkcí je postup, kterým se snažíme o nalezení nejjednoduššího vyjádření logické funkce, čímž rozumíme logickou funkci, která obsahuje nejmenší počet členů a každý člen obsahuje co nejmenší počet proměnných.
Kriteria minimalizace:
- Minimální počet logických operací (tj. počet realizačních prvků)
- Minimální počet proměnných (tj. počet vstupů realizačních prvků)
- Kombinaci obou předchozích kriterií pro zvolený (či danou technologií dovolený) soubor realizačních prvků.
Booleova algebra:
- Jedná se o soustavu pravidel určených k popisu vztahů mezi logickými proměnnými. Vzhledem k tomu, že argumenty logických proměnných nabývají pouze dvou hodnot, logické 0 či logické 1, je třeba Booleovu algebru chápat nikoliv jako algebru čísel, ale jako algebru stavů.
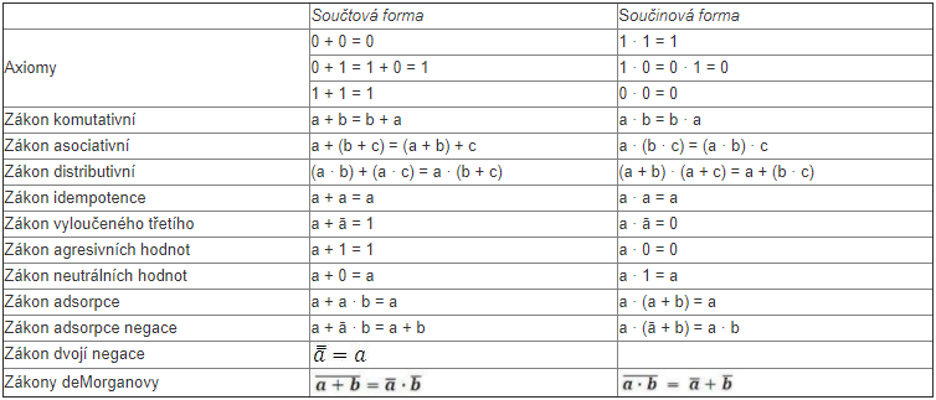
- Zákony Booleovy algebry budeme používat při minimalizaci logických funkcí. Všechny mají dvojí formu – součtovou a součinovou, které jsou duální, to znamená, že jedna forma vyplývá z druhé při záměně logického součtu (OR) za logický součin (AND) a současně hodnoty logické 0 za logickou 1.
- Na tomto místě je třeba připomenout, že logické spojky jsou rovnocenné, tedy že neexistuje přednost násobení před sčítáním známá z matematické algebry.
Minimalizace výrazů s využitím Karnaughových map:
- Karnaughovy mapy pro nás zatím představují nástroj pro grafické vyjádření logických funkcí. Hlavní význam map však spočívá v použití při jejich minimalizaci. To je umožněno základní vlastností Karnaughových map – totiž že se dvě sousední pole se liší v hodnotě pouze jedné proměnné.
- Připomeňme, že sousední pole jsou ta, která se dotýkají hranou, svislou či vodorovnou, a rovněž pole na protilehlých okrajích mapy:
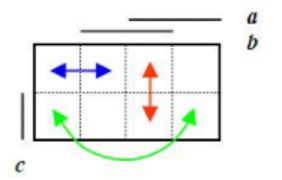
- Princip minimalizace pomocí map je následující: Obsahuje-li dvojice sousedních polí mapy logické 1, pak jim odpovídající součinové termy se liší pouze negací jedné logické proměnné. Tuto dvojici součinových termů lze nahradit jediným s počtem proměnných o jednotku menším tak, že se z obou vyloučí ona proměnná, která se liší v použití operace negace, podle zákona vyloučeného třetího: $a + \overline{a} = 1$ .
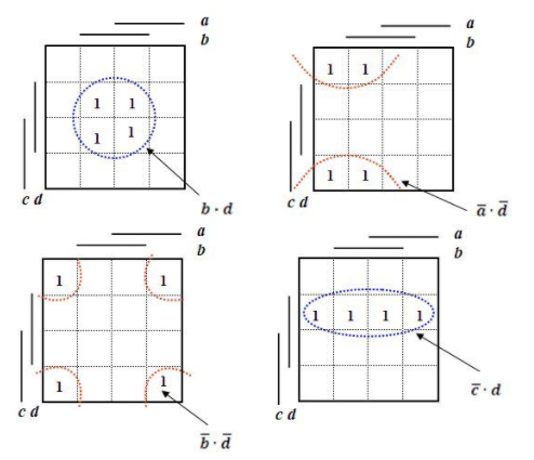
- Celý postup lze algoritmizovat s tím, že nebudeme hledat pouze dvojice sousedních polí obsahující logické 1, ale celé oblasti s počtem sousedních polí rovným mocnině dvou.
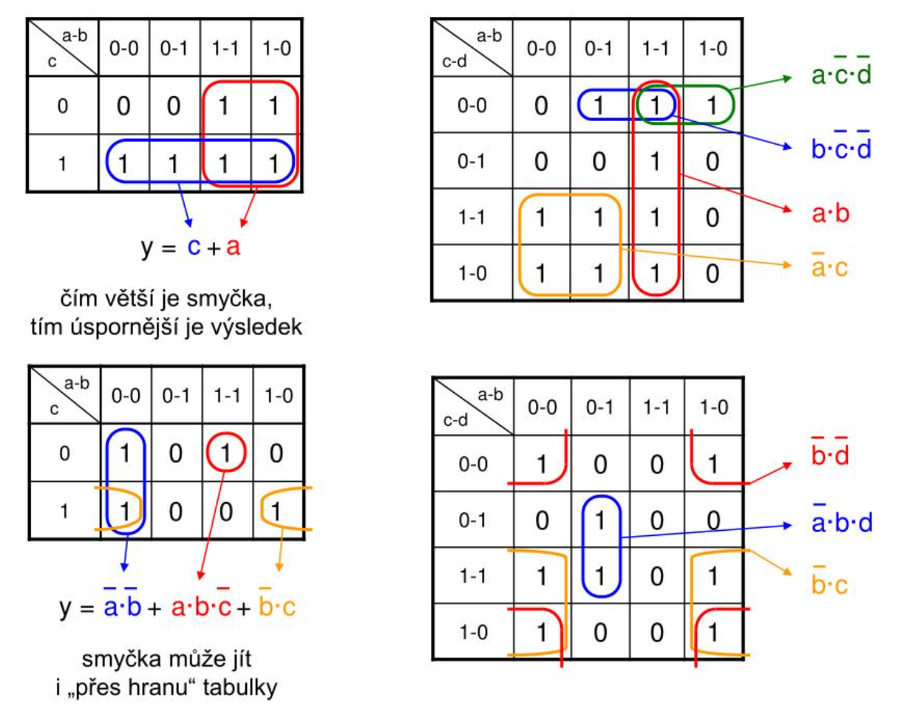
  1. Hledáme minimalizační smyčky, tj. takové oblasti mapy, které obsahují 2N polí s funkční hodnotou rovnou logické 1, přičemž každému poli přísluší v této smyčce N polí sousedních (neboli všechny „1“ uzavřeme do smyček ve tvaru čtverce či obdélníka o hranách délky 1, 2, 4, 8…)
  2. Snažíme se získat co nejmenší počet co největších minimalizačních smyček, které zahrnou všechna pole s funkční hodnotou logické 1.
  3. Minimalizační smyčky_ se mohou překrývat.
  4. Každá minimalizační smyčka generuje součinový term pouze těch proměnných, které mají pro všechna pole dané smyčky stejnou logickou hodnotu (a tedy je-li některá ze společných proměnných nulová, píše se s negací).
  5. Nakonec všechny součinové termy svážeme logickým součtem.